گاهی، استفاده از قانون اهم برای به دست آوردن ولتاژ و جریان مدارهای پیچیده، دشوار است. در نتیجه، برای انجام محاسبات مربوط به این مدارها به قوانینی نیاز داریم که بتوانیم بر اساس آن، معادلات مدار را به دست آوریم. قانون مداری شهف، یکی از راهحلهای مناسب برای این کار است.
در سال 1875، فیزیکدان آلمانی، «گوستاو شهف»، دو قانون بیان کرد که مربوط به جریان و انرژی در مدارهای الکتریکی بود؛ «قانون جریان شهف» (Kirchhoffs Current Law) یا KCL که مربوط به جریان در یک مدار بسته است و «قانون ولتاژ شهف» (Kirchhoffs Voltage Law) یا KVL که به ولتاژهای یک مدار بسته میپردازد.
قانون جریان شهف یا KCL بیان میکند: «جریان یا بار الکتریکی وارد شده به یک گره دقیقاً برابر با بار یا جریانی است که از آن خارج میشود». به عبارت دیگر، مجموع جبری تمام جریانهای وارد شده به یک گره باید برابر صفر باشد (I(exiting)+I(entering)=0I(exiting)+I(entering)=0). این ایده شهف، با نام پایستگی یا بقای بار نیز شناخته میشود.
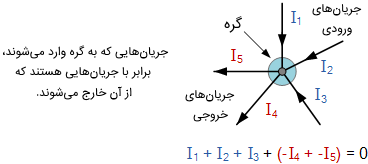
در شکل بالا، مقدار سه جریان I1I1، I2I2 و I3I3 که به گره وارد میشوند، مثبت است و دو جریان I4I4 و I5I5 که از گره خارج میشوند، منفی هستند. معادله زیر، رابطه بین جریانها را بیان میکند:
I1+I2+I3−I4−I5=0I1+I2+I3−I4−I5=0
اصطلاح گره در مدارهای الکتریکی معمولاً به اتصال یا پیوند دو یا بیشتر از دو مسیر حامل جریان مانند سیم یا قطعات الکتریکی اتلاق میشود. برای جریانی که به گره وارد یا از آن خارج میشود، باید یک مسیر بسته وجود داشته باشد. وقتی با تحلیل مدارهای موازی سر و کار داریم، میتوانیم از KCL استفاده کنیم.
قانون ولتاژ شهف یا KVL بیان میکند: «در هر شبکه حلقه بسته، کل ولتاژ حلقه برابر با مجموع تمام افت ولتاژهای موجود در آن است». به عبارت دیگر، مجموع تمام ولتاژهای حلقه باید برابر با صفر باشد. این ایده شهف، به عنوان بقا یا پایستگی انرژی نیز شناخته میشود.
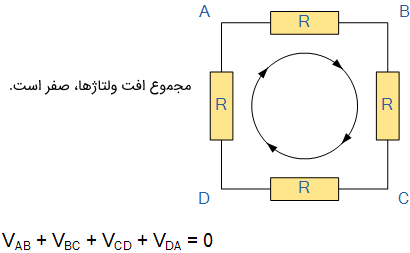
برای نوشتن معادله بر ولتاژ حلقه، باید از یک نقطه آن شروع کنیم، در یک جهت یکسان همه افت ولتاژها را بنویسیم و به همان نقطه اول باز گردیم. این نکته مهم است که وقتی افت ولتاژها را مینویسیم تغییر جهت ندهیم، زیرا با تغییر جهت، دیگر مجموع ولتاژها صفر نخواهد بود. از قانون ولتاژ شهف میتوان در مدارهای سری استفاده کرد.
وقتی یک مدار DC یا AC را با استفاده از قوانین مداری شهف تحلیل میکنیم، با واژهها و اصطلاحاتی روبرو میشویم که بخشهای مختلف مدار را توصیف می کنند، مانند گره، مسیر، شاخه، حلقه و مش. این اصطلاحات در مدارهای الکتریکی بسیار تکرار میشوند و دانستن آنها امری ضروری است.
شکل زیر گره، حلقه و شاخه را در یک مدار ساده نشان میدهد.
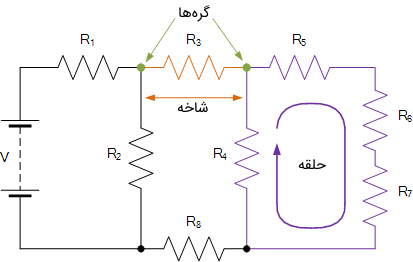
دقت کنید که میگوییم اجزیای مدار به صورت سری به هم متصل هستند، اگر جریان یکسانی از آنها بگذرد و میگوییم موازی هستند، اگر ولتاژ دو سر آنها برابر باشد.
در مدار شکل زیر، جریان گذرنده از مقاومت R3R3 را به دست آورید.
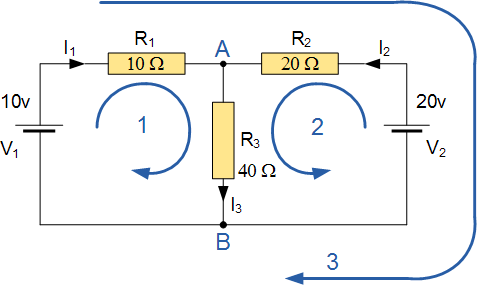
مدار 3 شاخه، 2 گره (A و B) و 2 حلقه مستقل دارد. با استفاده از قانون جریان شهف، معادلات زیر را داریم:
قانون ولتاژ شهف نیز منجر به معادلات زیر میشود:
از آنجایی که I3I3 برابر با مجموع I1+I2I1+I2 است، معادلات فوق را میتوان به صورت زیر بازنویسی کرد:
اکنون دو معادله داریم که میتوانیم با استفاده از آنها I1I1 و I2I2 را به دست آوریم. اگر محاسبات لازم را انجام دهیم، مقدار I1=−0.143I1=−0.143 و I2=+0.429I2=+0.429 آمپر به دست میآیند و از آنجایی که I3=I1+I2I3=I1+I2، مقدار I3=0.286AI3=0.286A است. ولتاژ دو سر مقاومت R3R3 نیز برابر است با: 0.286×40=11.44V0.286×40=11.44V.
علامت منفی جریان I1I1 به این معنی است که جهت اولیه جریان برای این حلقه اشتباه انتخاب شده بود. در حقیقت، باتری 20 ولتی، باتری 10 ولتی را شارژ میکند.
با کمک دو قانون مداری شهف میتوان مقادیر ولتاژ و جریان مدار را پیدا کرد. روند اصلی استفاده از این قوانین به صورت زیر است:
درباره این سایت