مدار الکتریکی، از به هم پیوستن قطعات الکتریکی غیرفعال (مقاومت، خازن، القاگر، لامپ، دیود و …) یا قطعات فعال (ترانزیستور و …)، یا ترکیبی از آن دو پدید می‌آید، چنان‌که دست کم یک مسیر بسته را ایجاد کنند تا جریان الکتریکی بتواند در این مسیر بسته جاری شود.

اگر قطعات تشکیل دهنده مدار، الکتریکی باشند، مدار الکتریکی نامیده می‌شود، و اگر برخی از قطعات، الکتریکی و برخی الکترونیکی باشند، مدار الکترونیکی است.

مدار های الکتریکی خطی نوعی از این مدار ها هستند که از یک منبع جریان یا ولتاژ و عناصر خطی همانند مقاومت تشکیل می شوند. جهت تحلیل این مدار ها می توان از روش هایی چون پاسخ فرکانسی و تبدیل لاپلاس استفاد کرد.

هر مدار الکتریکی از مؤلفه‌های زیر تشکیل شده‌است:

1. یک منبع تغذیۀ مانند باتری یا مولد
2. سیم‌ها یا نوارهای ارتباط دهندهٔ مدار، که از یک مادهٔ رسانای الکتریسیته خوب مانند مس ساخته می‌شوند.
3. قطعات مداری همچون خازن، مقاومت، القاگر، دیود، ترانزیستور و …

«آیرودینامیک» (Aerodynamics) را عموما می‌توان به حرکت اجسام مختلف در هوا مرتبط دانست. قوانین حاکم بر آیرودینامیک نشان می‌دهند که چگونه یک هواپیما قادر به پرواز است. تمام اجسامی که در هوا حرکت می‌کنند، تحت تاثیر قوانین حاکم بر آیرودینامیک قرار دارند. این اجسام می‌توانند یک موشک در حال انفجار یا یک بادبادک در حال پرواز و حتی یک ماشین مسابقه باشند. در واقع زمانی که یک جسم متحرک توسط هوا احاطه شده باشد، علم آیرودینامیک در مورد آن به کار می‌رود.

این مطلب به صورت دقیق، ابتدا به بررسی تعریف علم آیرودینامیک و تاریخچه پیدایش آن می‌پردازد. در ادامه، مفاهیم پرکاربرد و مهم آن مورد بررسی قرار می‌گیرند و در نهایت کاربردهای مختلف این علم با ذکر چند مثال بیان می‌شوند.

دید کلی

بنا بر قانون اول نیوتن اگر بر جسمی نیرو وارد نشود جسم یا ساکن می‌ماند و یا حرکت یکنواخت بر خط راست خواهد داشت. نتیجه آشکار قانون اول این است که اگر بر جسم نیرو وارد شود جسم ساکن نمی‌ماند و حرکت یکنواخت بر خط راست نیز خواهد داشت، در این صورت وارد کردن نیرو بر جسم در آن شتاب می‌دهد. قانون دوم نیوتن در واقع رابطه شتاب با نیرویی که بر آن وارد می‌شود را بیان می‌کند. شتاب جسمی به جرم m که نیروی F بر آن وارد می‌شود هم جهت و متناسب با نیروی وارد بر آن است و با جرم جسم نسبت عکس دارد. این بیان را می‌توان بصورت زیر نوشت:

 

a = F/m

F برآیند نیروهایی است که به علت اثر اجسام دیگر روی جسم مورد نظر وارد می‌شود. a شتاب آن و m جرم جسم است.


 

مفهوم قانون دوم نیوتن

جرم جسم به مقدار ماده‌ای که در ساختمان جسم بکار رفته است بستگی دارد رابطه بالا یک رابطه برداری است. و چون m یک کمیت نرده‌ای است و مثبت ، شتاب جسم هم جهت با نیروی وارد بر آن است. هر چه نیروی وارد بر یک جسم بزرگتر باشد شتاب آن نیز بزرگتر می‌شود، علاوه بر آن با یک نیروی معین هر چه جرم جسم بیشتر باشد شتاب آن یعنی تغییر در سرعتش کمتر خواهد بود. به عبارت دیگر با یک نیروی معین هر چه جرم جسم بیشتر باشد وضعیت حرکت بیشتر حفظ می‌شود، یعنی جسم ی بیشتری از خود نشان می‌دهند.

یک دروازه‌بان فوتبال می‌تواند با نیروی دست خود براحتی وضعیت حرکت توپ را تغییر دهد، ولی وی هرگز نمی‌تواند با دست خود و با همان نیرو ، وضعیت حرکت یک اتوبوس را تغییر دهد. آشکار است این تفاوت به علت جرم زیادتر اتوبوس نسبت به توپ فوتبال است، بنابراین می‌توان گفت اتوبوس بیش از توپ فوتبال ی دارد.

شتاب

برای یافتن شتاب یک جسم باید نیروهایی را که به آن وارد می‌شود معلوم باشد. در کارهای روزمره تنها نیروهای گرانشی و یا الکترومغناطیسی به اجسام وارد می‌شود و در نتیجه برای بدست آوردن شتاب جسم باید قوانین نیروی گرانش و یا نیروی الکترومغناطیسی وارد بر اجسام را بشناسیم. بردارهای F و a را می‌توانیم روی محورهای x و y تصویر کنیم، شتاب جسم در راستای معین مثلا راستای محور x صرفا مربوط به نیروی وارد بر جسم در همان راستا است. بنابراین با تجزیه نیروی وارد بر جسم روی دو محور بدست آوردن مؤلفه‌های نیرو می‌توان شتاب جسم روی هر یک از دو محور یعنی مؤلفه‌های شتاب را بدست آورد.


 

انتخاب دستگاه مختصات مناسب

می‌دانیم حرکت نسبی است، یعنی سرعت و شتاب اجسام نسبت به دستگاههای مختصات مختلف متفاوت است. به عنوان مثال یک اتومبیل را که با شتاب به راه می‌افتد در نظر بگیرد حرکت مسافر درون این اتومبیل نسبت به دستگاه مختصات متصل به جاده شتابدار است، اما همین مسافر نسبت به دستگاه مختصات که به خود اتومبیل متصل باشد ساکن است، یعنی شتاب ندارد. اما شتابی که در رابطه a = F/m برای جسم بدست می‌آید نسبت به کدام دستگاه مختصات است؟ یا اگر بخواهیم نیروی وارد بر یک جسم را تعیین کنیم، شتاب جسم نسبت به کدام دستگاه مختصات باید در نظر گرفته شود، دستگاه مختصات نام دارد.

در بسیاری از مسأله‌ها مثل حرکت اتومبیل ، هواپیما و . که سرعت اجسام زیاد نیست، می‌توان نشان داد که با تقریب خوبی دستگاه مختصات متصل به زمین یک دستگاه مختصات است. ولی این دستگاه برای بررسی حرکت اجسام سریع مانند موشکهای قاره پیما و یا موشکهایی که ماهواره‌ها را در مدار قرار می‌دهند، دستگاه مختصات نیست. بنابراین همواره شتاب اجسام را نسبت به دستگاه مختصات متصل به زمین در رابطه a = F/m قرار دهید.

اگر بر جسمی هیچ نیرویی اثر نکند (یعنی جسم دیگری با آن برهمکنش نداشته باشد) آن جسم به حرکت یکنواخت خود در راستای خط مستقیم ادامه می‌دهد، اگر جسم در ابتدا ساکن باشد در حال س باقی می‌ماند.

دید کلی

بررسی حرکت اجسام و یافتن اینکه چگونه یک حرکت بوجود می‌آید ذهن بشر را برای قرنها به خود مشغول کرده بود، اما توفیق چندانی در این مورد بدست نیامده بود. نیوتن با بهره گیری از هوش سرشار و تلاش بسیار خود با تدوین قوانین حرکت که به نام خود او اسم گذاری شده است، توانست قدمهای بزرگی بردارد و بسیاری از مسائل حرکت را با موفقیت زیاد حل کند. پیش از گالیه تصور می‌شد که حتی برای ادامه حرکت یکنواخت اجسام باید به آنها نیرو وارد کرد.
 

ین تصور از برداشت غیر مو شکافانه حرکت اجسام در زندگی روزمره ناشی می‌شد. به تجربه ثابت شده بود که اگر از هل دادن صندوقی که روی سطحی افقی با سرعت ثابت حرکت می‌کند دست بردارند، یعنی به آن نیرو وارد نکنند صندوق از حرکت باز می‌ایستد. گالیله با انجام آزمایش و پس از آن نیز با تعمیم ذهنی نتایج آزمایش ،‌ نخستین کسی بود که در این تصور عمومی تردید کرد. نیوتن که در سال مرگ گالیله به دنیا آمد بررسیهای دقیق درباره حرکت انجام داد و قوانین حرکت را استخراج کرد.

آزمایش

بنا به تعریف هیچ نیرویی نباید بر جسم اثر کند اما حداقل نیروی گرانش زمین بر جسم اثر خواهد کرد و نمی‌توان آنرا از میان برد. با استفاده از وسایل آزمایشگاهی مخصوص می‌توان شرایطی فراهم کرد که بجز در راستای قائم حداقل نیروی گرانش کره زمین بر جسم اثر می‌کند، در کلیه جهتهای افقی تقریبا نیرویی بر جسم اثر نکند در نتیجه به کمک این وسایل می‌توان قانون اول نیوتن را در جهت افقی با تجربه آزمود. یکی از وسایل تخت هواست، تخت هوا از محفظه‌ای به شکل مکعب مستطیل ساخته شده است که روی آن تعدادی سوراخ ریز وجود دارد. در هنگام آزمایش باید سطح آن کاملا افقی باشد هوا با سرعت وارد محفظه شده و از تمام سوراخها خارج می‌شود.

اگر مهره‌ای روی تخت هوا قرار دهیم لایه نازکی از هوا میان مهره و سطح تخت هوا تشکیل می‌شود و تماس نزدیک مهره با سطح تخت هوا از میان می‌رود. به این ترتیب اصطکاک میان مهره و سطح تخت هوا بسیار کوچک می‌شود. در نتیجه در کلیه جهتهای افقی تقریبا نیروی بر جسم وارد نمی‌شود، اگر به مهره سرعت کمی داده شود تا کناره تخت هوا در امتداد خط مستیقم و با همان سرعت پیش می‌رود و به این ترتیب قانون اول نیوتن در جهت افقی با آزمایش تأیید می‌شود. ملاحظه می‌شود که حرکت جسم در امتداد خط مستقیم و افقی با سرعت ثابت نیازی به نیرو ندارد.

قانون ی

یک کشتی فضایی در فضای میان ستاره‌ها و با فاصله بسیار زیاد در آنها با هیچ چیزی برهمکنش ندارد. اگر این کشتی فضایی موتور خود را خاموش کند طبق قانون اول نیوتن در امتداد یک خط راست با سرعت ثابت حرکت می‌کند و مفهوم قانون ی این است که اگر بر جسمی نیرو وارد نشود جسم مایل است وضعیت حرکت خود را حفظ کند. این خاصیت از اجسام که میل دارند وضعیت حرکت خود را در غیاب نیرو حفظ کنند ی نامیده می‌شود. از اینرو قانون اول نیوتن قانون ی نیز نامیده می‌شود و چارچوبهای مرجعی که این قانون در آنها بکار می‌رود چارچوبهای نام دارند، این چارچوبها نسبت به ستاره‌های دور ثابت فرض می‌شوند.

نتایج قانون اول نیوتن

• در این قانون تفاوتی میان جسم ساکن و جسمی که با سرعت ثابت حرکت می کند وجود ندارد، هر دو حرکت در غیاب نیرو طبیعی‌اند، دلیل این امر وقتی روشن می‌شود که جسم ساکن در یک چارچوب مرجع ، مرجع دیگری که با سرعت ثابت نسبت به اولی حرکت می‌کند مشاهده کنیم. ناظری که در چارچوب اول قرار دارد جسم را در حال س می‌بینید و ناظر واقع در چارچوب دوم می‌بیند که همان جسم با سرعت یکنواخت در حال حرکت است. هر دو ناظر متوجه می‌شوند که جسم شتاب ندارد یعنی سرعت آن تغییر نمی‌کند و هر دو از قانون اول نتیجه می‌گیرند که هیچ نیرویی بر جسم وارد نمی‌شود.
   
• میان نبودن و بودن نیروهایی که برآیندشان صفر است تفاوتی وجود ندارد. مثلا اگر فشار دستها به کتاب نیروی اصطکاک را کاملا خنثی کند کتاب با سرعت یکنواخت حرکت می‌کند، بنابراین راه دیگر بیان قانون اول این هست که اگر در مجموع نیرویی بر جسم اثر نکند شتاب آن صفر است.

گاهی، استفاده از قانون اهم برای به دست آوردن ولتاژ و جریان مدارهای پیچیده، دشوار است. در نتیجه، برای انجام محاسبات مربوط به این مدارها به قوانینی نیاز داریم که بتوانیم بر اساس آن، معادلات مدار را به دست آوریم. قانون مداری شهف، یکی از راه‌حل‌های مناسب برای این کار است.

 در سال 1875، فیزیکدان آلمانی، «گوستاو شهف»، دو قانون بیان کرد که مربوط به جریان و انرژی در مدارهای الکتریکی بود؛ «قانون جریان شهف» (Kirchhoffs Current Law) یا KCL که مربوط به جریان در یک مدار بسته است و «قانون ولتاژ شهف» (Kirchhoffs Voltage Law) یا KVL که به ولتاژهای یک مدار بسته می‌پردازد.

قانون اول شهف؛ قانون جریان (KCL)

قانون جریان شهف یا KCL بیان می‌کند: «جریان یا بار الکتریکی وارد شده به یک گره دقیقاً برابر با بار یا جریانی است که از آن خارج می‌شود». به عبارت دیگر، مجموع جبری تمام جریان‌های وارد شده به یک گره باید برابر صفر باشد (I(exiting)+I(entering)=0I(exiting)+I(entering)=0). این ایده شهف، با نام پایستگی یا بقای بار نیز شناخته می‌شود.

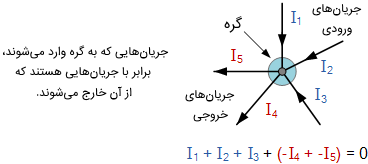
در شکل بالا، مقدار سه جریان I1I1، I2I2 و I3I3 که به گره وارد می‌شوند، مثبت است و دو جریان I4I4 و I5I5 که از گره خارج می‌شوند، منفی هستند. معادله زیر، رابطه بین جریان‌ها را بیان می‌کند:

I1+I2+I3−I4−I5=0I1+I2+I3−I4−I5=0

اصطلاح گره در مدارهای الکتریکی معمولاً به اتصال یا پیوند دو یا بیشتر از دو مسیر حامل جریان مانند سیم یا قطعات الکتریکی اتلاق می‌شود. برای جریانی که به گره وارد یا از آن خارج می‌شود، باید یک مسیر بسته وجود داشته باشد. وقتی با تحلیل مدارهای موازی سر و کار داریم، می‌توانیم از KCL استفاده کنیم.

قانون دوم شهف؛ قانون ولتاژ (KVL)

قانون ولتاژ شهف یا KVL بیان می‌کند: «در هر شبکه حلقه بسته، کل ولتاژ حلقه برابر با مجموع تمام افت ولتاژهای موجود در آن است». به عبارت دیگر، مجموع تمام ولتاژهای حلقه باید برابر با صفر باشد. این ایده شهف، به عنوان بقا یا پایستگی انرژی نیز شناخته می‌شود.

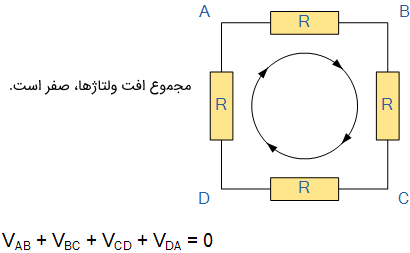
برای نوشتن معادله بر ولتاژ حلقه، باید از یک نقطه آن شروع کنیم، در یک جهت یکسان همه افت ولتاژها را بنویسیم و به همان نقطه اول باز گردیم. این نکته مهم است که وقتی افت ولتاژها را می‌نویسیم تغییر جهت ندهیم، زیرا با تغییر جهت، دیگر مجموع ولتاژها صفر نخواهد بود. از قانون ولتاژ شهف می‌توان در مدارهای سری استفاده کرد.

وقتی یک مدار DC یا AC را با استفاده از قوانین مداری شهف تحلیل می‌کنیم، با واژه‌ها و اصطلاحاتی روبرو می‌شویم که بخش‌های مختلف مدار را توصیف می کنند، مانند گره، مسیر، شاخه، حلقه و مش. این اصطلاحات در مدارهای الکتریکی بسیار تکرار می‌شوند و دانستن آن‌ها امری ضروری است.

اصطلاحات مدارهای DC

• مدار (Circuit): یک مدار، مسیر هادی حلقه بسته‌ای است که  جریان الکتریکی در آن برقرار می‌شود.
• مسیر (Path): یک خط از عناصر یا منابع متصل به هم است.
• گره (Node): گره، یک اتصال یا پیوند از مدار است که در آن، دو یا بیشتر از دو عنصر مدار به هم متصل هستند. گره را با یک نقطه مشخص می‌کنیم.
• شاخه (Branch): شاخه، یک یا گروهی از اجزای مدار مانند مقاومت یا منبع است که بین دو گره وصل شده‌اند.
• حلقه (Loop): حلقه، یک مسیر بسته در مدار است که اگر از یک نقطه شروع کنیم و به همان جا برگردیم، بیش از یک بار از هر عنصر عبور نکرده باشیم.
• مش (Mesh): مش، ساده‌ترین حلقه مدار است که شاخه‌ای در آن نیست.

شکل زیر گره، حلقه و شاخه را در یک مدار ساده نشان می‌دهد.

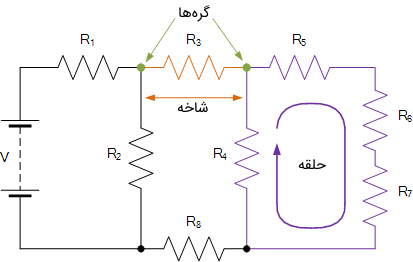
دقت کنید که می‌گوییم اجزیای مدار به صورت سری به هم متصل هستند، اگر جریان یکسانی از آن‌ها بگذرد و می‌گوییم موازی هستند، اگر ولتاژ دو سر آن‌ها برابر باشد.

مثال

در مدار شکل زیر، جریان گذرنده از مقاومت R3R3‌ را به دست آورید.

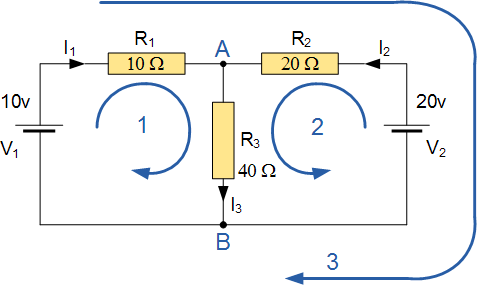
مدار 3 شاخه، 2 گره (A و B) و 2 حلقه مستقل دارد. با استفاده از قانون جریان شهف، معادلات زیر را داریم:

• در گره A: I1+I2=I3I1+I2=I3
• در گره B: I3=I1+I2I3=I1+I2

قانون ولتاژ شهف نیز منجر به معادلات زیر می‌شود:

• حلقه 1: 10=R1I1+R3I3=10I1+40I310=R1I1+R3I3=10I1+40I3
• حلقه 2: 20=R2I2+R3I3=20I2+40I320=R2I2+R3I3=20I2+40I3
• حلقه 3: 10−20=10I1−20I210−20=10I1−20I2

از آنجایی که I3I3 برابر با مجموع I1+I2I1+I2 است، معادلات فوق را می‌توان به صورت زیر بازنویسی کرد:

• معادله اول: 10=10I1+40(I1+I2)=50I1+40I210=10I1+40(I1+I2)=50I1+40I2
• معادله دوم: 20=20I2+40(I1+I2)=40I1+60I220=20I2+40(I1+I2)=40I1+60I2

اکنون دو معادله داریم که می‌توانیم با استفاده از آن‌ها I1I1 و I2I2 را به دست آوریم. اگر محاسبات لازم را انجام دهیم، مقدار I1=−0.143I1=−0.143 و I2=+0.429I2=+0.429‌ آمپر به دست می‌آیند و از آن‌جایی که I3=I1+I2I3=I1+I2، مقدار I3=0.286AI3=0.286A است. ولتاژ دو سر مقاومت R3R3 نیز برابر است با: 0.286×40=11.44V0.286×40=11.44V.

علامت منفی جریان I1I1‌ به این معنی است که جهت اولیه جریان برای این حلقه اشتباه انتخاب شده بود. در حقیقت، باتری 20 ولتی، باتری 10 ولتی را شارژ می‌کند.

کاربرد قوانین مداری شهف

با کمک دو قانون مداری شهف می‌توان مقادیر ولتاژ و جریان مدار را پیدا کرد. روند اصلی استفاده از این قوانین به صورت زیر است:

1. فرض کنید همه ولتاژها و مقاومت‌ها داده شده‌اند (اگر داده نشده باشند، آن‌ها را نامگذاری کنید، مثلاً V۲ ،V۱ و … و R۲ ،R۱ و …).
2. هر شاخه مدار را به عنوان شاخه جریان در نظر بگیرید و نامگذاری کنید (I1I1، I2I2، I3I3 و غیره).
3. معادلات قانون اول شهف را برای هر گره بنویسید.
4. معادلات قانون دوم شهف را برای حلقه‌های مستقل مدار بنویسید.
5. از معادلات خطی به دست آمده استفاده کرده و جریان‌های نامعلوم را بیابید.